TF例子
文本相关性,最常见的场景就是搜索后的排序。比如我想团购一个火锅店,搜索“火锅”关键词后有如下两段店家的描述。其中第一家是火锅店,第二家是做“烧鸡公”的。
1.重庆有面儿火锅店面色彩温馨,装修精致,宽敞,老板、服务人员热情,让您能真正酣畅淋漓的感受老火锅的火辣热情。
2.重庆“烧鸡公”最先出自于重庆璧山县。据说是一帮司机哥们出了一趟长途车,饿得如狼似虎,好不容易看见前不着村,后不着店的地方有一老字号餐馆,上前一问老板都关门了,什么也没有了,说尽好话,老板只好将就把自己养的鸡宰了,又加了大量的辣椒和香料,还有剩余的火锅底料一起烧,没想到这一烧,就烧出了一道名菜,从此风靡川渝两地。
诶,其实凭借我们的直觉就发现,一段描述中如果搜索命中的词出现的越多,就越可能是我们想要的结果。这就是词频TF(Term Frequency)。同样是如上的,两段文字,如果是搜索的“重庆 老火锅”两个关键词,结果又会是怎样的呢?
3.重庆有面儿火锅店面色彩温馨,装修精致,宽敞,老板、服务人员热情,让您能真正酣畅淋漓的感受老火锅的火辣热情。
4.重庆“烧鸡公”最先出自于重庆璧山县。据说是一帮司机哥们出了一趟长途车,饿得如狼似虎,好不容易看见前不着村,后不着店的地方有一老字号餐馆,上前一问老板都关门了,什么也没有了,说尽好话,老板只好将就把自己养的鸡宰了,又加了大量的辣椒和香料,还有剩余的火锅底料一起烧,没想到这一烧,就烧出了一道名菜,从此风靡川渝两地。
根据这个观察,我们发现,如果某些词在所有文档都出现(这里是“重庆”),那么排序过程中这个词就不具有区分度了。换言之,在搜索的所有店家的描述中,出频度越大的,重要性就会降低,其实也就是一个近似反比关系。也就是IDF(Inverse Document Frequency)
TF-IDF
设定一个搜索为query,一个店家的描述为文档document。对各个内容进行分词后,任何一段落就都是词频构成的集合了。可以把query和单个document分别表示成如下形式:
query= (qtf 1,...,qtf |M1|) document = (tf 1,...,tf |M2|)
假设在搜索的过程中,documents的总量为N,出现query相应关键词的documents数量为n。
那么用于排序计算的相关性就可以定义为:
TF-IDF = tf(qt,d) × log (N/n)
tf(qt,d)代表qt这个词在文档d中出现的次数。其中加上log就是为了降低N/n对整个相关性的影响,因搜索过程中N往往远远大于n,而一个在文档中出现的TF却不是远远小于document的长度。而其物理意义这是信息理论中定义:如果随机的一个文档D包含一个词qt的概率p,那么“D包含qt”所含的信息量就是-log(p),也就是-log(n/N)。按照这个方式计算文档3和文档4相对于搜索关键词的相关性,看是否符合预期:
重庆:文档3(1×0) 文档4(2×0)
老火锅:文档3(1×log2) 文档4(0×?)
其本符合预期,“重庆”不具有区分度,老火锅在文档3中所占比重更大。但现在有一个问题就是TF-IDF没办法定义n为0的情况,就像上面写上问号的地方。如何让一个定义的公式覆盖所有情况呢?先留下这个疑问。我们再来看看另外一个例子。搜索“重庆 火锅”这关键字:
5.重庆有面儿火锅店面色彩温馨,装修精致,宽敞,老板、服务人员热情,让您能真正酣畅淋漓的感受老火锅的火辣热情。
6.重庆“烧鸡公”最先出自于重庆璧山县。据说是一帮司机哥们出了一趟长途车,饿得如狼似虎,好不容易看见前不着村,后不着店的地方有一老字号餐馆,上前一问老板都关门了,什么也没有了,说尽好话,老板只好将就把自己养的鸡宰了,又加了大量的辣椒和香料,还有剩余的火锅底料一起烧,没想到这一烧,就烧出了一道名菜,从此风靡川渝两地。
BM25
按照之前TF-IDF的定义,这两个文档的TF-IDF岂不是都为0且相等了?!但明明文档5讲的是火锅,第二个讲的是烧鸡公啊!这时你还发现什么?文档6长度更长,虽然同样出现了“火锅”字样,但它其他很多部分讲的就是跟“鸡”相关的。这时我们想到,文档越长,同样的单个词,能表现这个文档主题的能力就变弱了。所以我们应该在文档长度考虑进相关性里来,而且也是一个反比性关系。那我可不可以就把TF除上一个文档长度?但实际上并没这么简单,我们应该考虑一个平均文档长度avdl(average document length)。在所有的文档中,如果一个文档的长度dl(词的总数而非字数)大于avdl的时候才应当处罚。于是我们可以考虑:
\[\frac{tf}{\frac{dl}{avdl}}\]tf/(dl/avdl)
但是文档长度真的有影响么?我们能否加一个参数进行调节?如下b取值[0,1]区间。
\[B = (1 - b ) + b\frac{dl}{avdl}\]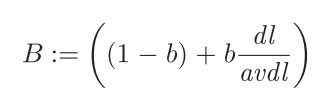
那么我们就用tf/B岂不就好了?b取0时文档长度无作用,取1时表示完全起作用,取0.5时表示有可能起作用有可能不起作用。但我们更偏向于相信文档长度是作用的,那么我们取一个0.75
而且我们再次发现,TF-IDF中,TF是一个整数,乘积结果会如下图最左面那样成阶梯形跳跃,数据不连续。而且会有一个很大的问题,乘积结果会没有上限。
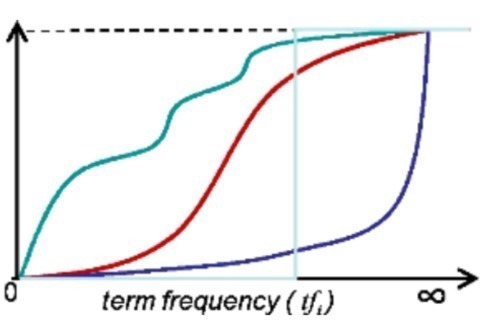
那能不能把这个乘积做得更平滑一些,并且作归一化呢?如下图:
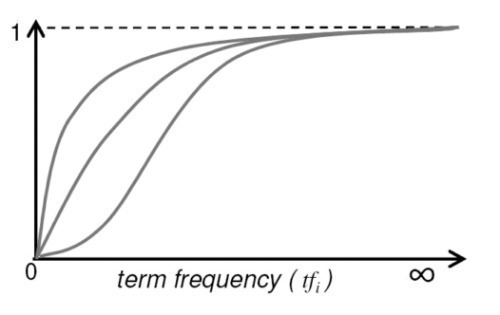
前人很巧妙的想到了把TF作如下变化:
\(\frac{tf}{k+ tf},\quad \text{其中k>0}\)
tf /(k+ tf) , 其中k>0
其中当k=1时,tf>=1的情况也可以占据[0,1)区间中一半;而当k=2时,tf>=1的情况也可以占据[0,1)区间的3/2,这样能更好的利用[0,1)区间进行表征所有TF的情况。
TF进行了相关优化,IDF是否也能进行相关优化呢?之分母不能为0,那我分母加上一个值不就可以搞定了?但就算加上1,在物理意义上就表示包含这个term的文档多了一个,会不会影响IDF意义的表征?那好,那我们就加一个0.5。相关的推理,也就可以参考Robertson/Sprck Jones weight的推导。
\[IDF(q_i) = log\frac{N - n(q_i) + 0.5}{n(q_i)+ 0.5},\quad\text{Robertson/Sprck Jones weight}\]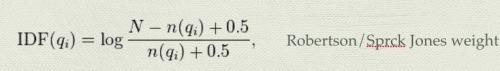
好了,这下该把演进后的TF-IDF搬上荧幕了:
\[\begin{aligned} {tf'} & = \frac{tf}{B} \\ {BM25_i(tf)} & = \frac{tf'}{k_1+tf'} IDF_i \\ & = \frac{tf}{k_1((1-b)+b\frac{dl}{avdl})+tf} IDF_i \end{aligned}\]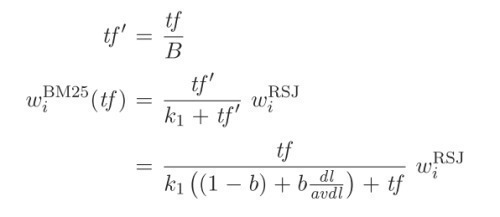
最终公式
那就是BM25:
\[score(D,Q) = \sum_{i=1}^n IDF(q_i) \cdot \frac{f(q_i,D) \cdot (k_1 + 1)}{f(q_i,D) + k_1 \cdot (1 - b + b \cdot \frac{|D|}{avgdl})} \]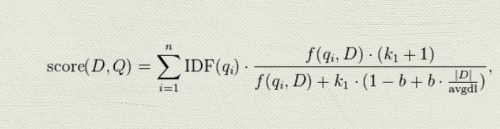
其中qi代表一个query Q中的其中一个词(TF-IDF其实只能算一个词跟一个文档的相似度),D就代表某个文档,|D|就是文档长度。其中最常取的值就是k1=2,b=0.75。
References:
Robertson, S. (2010). The Probabilistic Relevance Framework: BM25 and Beyond. Foundations and Trends® in Information Retrieval (Vol. 3, pp. 333–389). doi:10.1561/1500000019
Original post: http://blog.josephjctang.com/2014-08/bm25/